System Identification
Methods
ISC uses a range of methods of different complexity to estimate model parameters or identify systems:
- Least-Squares Estimation (online and offline)
- Extended Kalman Filtering (EKF, online and offline)
- Simulation-based optimisation (offline parameter estimation)
The method used depends on the properties of the system and whether offline estimation is sufficient or whether online estimation is required.
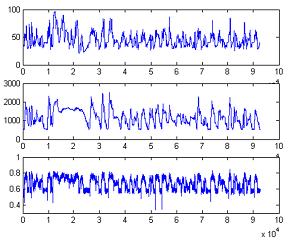
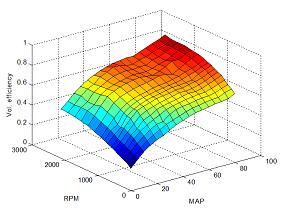
Volumetric Efficiency LUT Generated from the Time Series Estimated using the EKF
Grey-Box Modelling
Many control design projects involve the development a nonlinear dynamic model to capture the behaviour of the plant/process, in a level of detail that is appropriate for the controller to be designed. In many systems, there is insufficient knowledge about the plant to model every relevant physical detail mathematically (i.e. white-box modelling). On the other hand, purely considering I/O data to derive the plant dynamics without (using) any knowledge of the structure of those dynamics (i.e. black-box modelling) can lead to over-simplification and a bias towards the specific conditions under which data were obtained.
Our recommended model type is usually a grey-box model, where the main plant structure and well-known subsystems are defined mathematically as white-box models, and the remaining subsystems defined as black-box models. In the latter case, we still use as much knowledge of the interactions between the subsyetm inputs, outputs and internal variables as possible in establishing the model structures.
The 'greyness' of models can vary considerably from those where the structure and some parameters are known precisely from physical principles or measurements (e.g. masses and dimensions) and only a few parameters need to be estimated, to those where there is only a basic knowledge of the number of states and I/O relations. In the latter case, the system identification may need to include the determination of e.g. the optimal number of states or the optimal order of a polynomial.
Example Projects
- Online EKF estimation of the coefficients of friction models of a servo system (including judder and stick-slip motion) - The friction models were Dahl and LuGre models. The estimation algorithm and software were first tested in simulation, with known friction models, and then applied to test data from the real servo-mechanism.
- Estimation of the kinetic parameters of a Selective Catalytic Reduction (SCR) system (for an automotive diesel engine) - The estimation had to be performed online to capture the time-varying effects of aging effects, using limited measurement data. To enable the estimation to run on a standard automotive Electronic Control Unit (ECU), the algorithm had to be relatively simple. A modified Gauss-Newton method was selected.
Need assistance in system identification?
Interested in system identification training?
